忍野(おしの) ニャ

人工智能复习

笔记 ·2019-12-25·733阅读

封面 ID:78296283
使用教材《人工智能原理与应用》第二版，张仰森
PDF下载，仅供参考

绪论

定义：具有智能行为的计算机系统

人工智能诞生的标志发展阶段：1956年的达特茅斯会议，McCarthy 总结人工智能

主要研究方法：

  • 自上而下，符号主义（逻辑演绎）
  • 自下而上，连接主义（模拟神经元）
  • 行为主义（人工智能会自己进化，无需知识和推理）

主要研究领域：（知道五六个）

  • 专家系统
  • 自然语言处理
  • 机器学习
  • 自动定理证明
  • 自动程序设计
  • 分布式人工智能
  • 机器人
  • 模式识别
  • 博弈
  • 计算机视觉
  • 人工神经网络

知识表示

知识特性：相对正确性（范围有效）、不确定性（模糊性）、可表示性（可数据化存储处理）、可利用性

逻辑表示

表示知识步骤：

  1. 定义谓词，确定谓词语义
  2. 对每个谓词中的变元赋以待定的值
  3. 通过谓词的连接表示规则

例子：机器人在c处；a、b处各有一个桌子且a处桌子上有箱子，现在要机器人到a把箱子搬到b再回原点

TABLE(x):x是桌子。        ON(w,x):w在x的上面。 
EMPTY(y):y手中是空的。    AT(y,z):y在z处。
HOLDS(y,w):y拿着w。       GOTO(x,y):从x走到y。
PICK_UP(x):在x处拾起积木。SET_DOWN(x):在x处放下积木。

初始状态描述：
AT(robot,c),EMPTY(robot),TABLE(a),TABLE(b),ON(box,a)
目标状态描述：
AT(robot,c),EMPTY(robot),TABLE(a),TABLE(b),ON(box,b)

规则：
GOTO(x,y)
  条件：AT(robot,x)
  动作：删除 AT(robot,x)，增加 AT(robot,y)
PICK_UP(x) 
  条件：AT(robot,x)∧EMPTY(robot)∧TABLE(x)∧ON(box,x)
  动作：删除 EMPTY(robot) ON(box,x)，增加 HOLDS(robot,box)
SET_DOWN(x) 
  条件：AT(robot,x)∧HOLDS(robot,box)∧TABLE(x)
  动作：删除 HOLDS(robot,box)，增加 EMPTY(robot) ON(box,x)

优缺点

  • + 类自然语言、易实现、精确性、推理严密模块化
  • - 不能表示不确定知识、组合爆炸问题、过程复杂效率低

产生式系统

产生式系统由数据库（初始条件，中间结果）、规则库（if x then y）、推理机（规则选择）构成。可用于确定性/不确定性表示

表示方法

  • 确定性规则知识 if p then q
  • 非确定性规则知识 if p then q (可信度)
  • 确定性事实性知识（对象，属性，值）/（关系，对象1，对象2）
  • 确定性事实性知识（对象，属性，值，可信度）/（关系，对象1，对象2，可信度）

推理方式

  • 正向推理，适合初始状态数小于目标数
  • 反向推理，适合初始状态数大于等于目标状态数
  • 双向推理

产生式特点：清晰性（规则形式固定且独立）、模块性（知识库和推理机分离）、自然性（符合人的思维）

语义网络

语义网络是一个有向图，节点表示实体，弧表示节点之间的关系（动作/属性）

常用语义关系

  • 类属关系：具有共同属性的不同事物，如 AKO、AMO、ISA
  • 包含关系：部分与整体，Part-of
  • 占有关系：事物或属性间的“具有”关系，Have
  • 时间关系：事件发生时间先后，before、after、during

推理过程

  • 匹配推理：根据问题构造局部网络，求解部分留空；从知识库中寻找相近的网络；留空处匹配的结果就是解
  • 继承推理：值继承（直接继承上层节点的属性）、过程继承（继承属性的计算方法）

语义网络特点：结构性、自然性、联想性（事物联系）、非严格性（表示形式不唯一）

框架结构

框架名：每个框架都要拥有框架名。
槽：用于描述对象的某一方面的属性，并且可以设置约束条件。
侧面：用于描述相应属性的一个方面。
有些属性是事先确定的(类属特性)，有些属性值需要在生成实例的时候代入。

框架的匹配就是实体代入框架的过程。其推理方法遵循匹配和继承原则，主要有匹配推理和演绎推理
匹配推理：将问题框架表示，求解部分留空；与知识库中的框架匹配选出候选框架；对候选框架评价选出结果，留空处匹配的结果为解

框架特点：结构性、继承性、自然性

谓词演算与消解原理

置换&合一

置换是形如${t_1/x_1\cdots t_n/x_n}$的有限集，前者只含常量，后者只含变量，表示用前者替换后者

有$\theta={a_1/x_1\cdots a_n/x_n},\lambda={b_1/y_1\cdots b_n/y_n}$，则 θλ 如下求得
$$tmp={a_1\cdot\lambda/x_1\cdots a_n\cdot\lambda/x_n}\cup\lambda$$
先从 λ 中删除 $y_i\in{x_1\cdots x_n}$ 的项，再删除 $a_i\cdot\lambda=x_i$ 的项，剩下的 tmp 就是 θλ

有公式集${E_1\cdots E_n}$，若存在置换 θ 使得$E_1\lambda=\cdots=E_n\lambda$，则该公式集可合一，θ 为合一置换

最一般合一置换(mgu)不唯一，若存在公式 E1 和 E2，他们的 mgu 求法如下

  1. 令 $W={E_1,E_2}$
  2. 令 $k=0,W_k=W,\sigma_k=\epsilon$，$\epsilon$ 指空置换
  3. 如果 $W_k$ 只剩一个，停止算法，$\sigma_k$ 为所求
  4. 求 $W_k$ 的不一致集 $D_k={a_k,x_k}$
  5. $\sigma_{k+1}=\sigma_k\cdot {a_k/x_k},W_{k+1}=W_k{a_k/x_k},k=k+1$，然后转第三步

消解反驳

skolem范式是消去存在量词的前束范式（合取），消除存在量词规则：

  • 存在量词不在全称量词辖域：直接用某个常量代替
  • 存在量词在若干个全称量词的辖域：用$f(x_i\cdots)$代替存在量词约束的变量，$x_i$为受到的全称约束变量

原子公式/原子：不含连接词的谓词公式
文字：原子及原子的否定；
子句：文字的析取式
通过 skolem 化获取，其合取项的集合就是一子句集

归结公式（关键找到互补文字）：
$$\lambda\lor C_1,\neg\lambda\lor C_2 \rightarrow C_1\lor C_2$$
消解反驳：若要从子句集 S 中推出 λ，等价于从 $S\cup{\neg\lambda}$ 中推出恒假 NIL。互补文字中允许常量置换变量
消解反驳问题求解：将待求解问题用谓词公式表示，将其否定并与Answer谓词构成析取式加入到原子句集中消解

消解原理改进：

  • 广度优先：每个子句要跟其他子句消解。可以保证找到最短消解路径但是有组合爆炸的问题
  • 支集策略：略
  • 单位优先：优先使用单位子句

非确定性推导

证据：已知事实；知识：规则
不确定性方法分类：模型方法（不确定的证据和不确定的知识算出结论的不确定性）、控制方法

可信度方法

知识以产生式规则的形式表示，知识不确定性以可信度 CF(H,E) 表示，通常由专家给出
$$if\quad E\quad then\quad H, \quad CF(H,E)$$
其中 E 可以是复合条件，H 可以多个结论

证据不确定性以 CF(E) 表示，初始给出或推导算出。当证据是多个证据的合取时，其 CF 取当中的最小；析取时取最大
$$
\begin{aligned}
E&=E_1\wedge\cdots\wedge E_n\
CF(E)&=min{CF(E_1)\cdots CF(E_n)}
\end{aligned}
$$

推理计算：

  • 单条知识支持结论：$CF(H)=CF(H,E)*max{0,CF(E)}$
  • 多条知识支持同一结论（假设两条）：
    • 先用上面的方法分别计算每一条知识的结论可信度得到 $CF_1(H),CF_2(H)$
    • 然后使用以下公式进行合成

$$CF_{1,2}(H)=
\begin{cases}
CF_1(H)+CF_2(H)-CF_1(H)CF_2(H)\quad &if\ CF_1(H)\ge 0,CF_2(H)\ge 0\
CF_1(H)+CF_2(H)+CF_1(H)CF_2(H)\quad &if\ CF_1(H)<0,CF_2(H)<0\
{CF_1(H)+CF_2(H)\over 1-min(|CF_1(H)|,|CF_2(H)|)}\quad &if\ CF_1(H)*CF_2(H)<0
\end{cases}
$$

已知道结论原始可信度 CF(E) 的情况下更新 得到 CF(H/E)：
当 CF(E)>0
$$CF(H/E)=
\begin{cases}
CF(H)+CF(H,E)CF(E)-CF(H)CF(H,E)CF(E)\quad &if\ CF(H)\le 0,CF(H,E)\le 0\
CF(H)+CF(H,E)CF(E)+CF(H)CF(H,E)CF(E)\quad &if\ CF(H)<0,CF(H,E)<0\
{CF(H,E)CF(E)+CF(H)\over 1-min(|CF(H)|,|CF(H,E)CF(E)|)}\quad &if\ CF(H)*CF(H,E)<0
\end{cases}
$$
当 CF(E)=0 不用更新

主观Bayes

推理网络是一个有向图，节点表示假设结论，边表示规则并且有一数值对 (LS,LN)，分别代表规则成立的充分性和必要性。

知识不确定性由 (LS,LN) 描述，表现为
$$if\quad E\quad then\ (LS,LN)\ H\ [P(H)]$$
证据不确定性由概率 P(E/S) 描述（但计算用C(E/S)），当证据是多个证据的合取时，其 P 取当中的最小；析取时取最大
$$
\begin{aligned}
E&=E_1\wedge\cdots\wedge E_n\
P(E/S)&=min{P(E_1/S)\cdots P(E_2/S)}
\end{aligned}
$$

推理计算
Ⅰ确定性证据：

  • 证据肯定出现 P(E)=P(E/S)=1 时：$P(H/E)={LSP(H)\over (LS-1)P(H)+1}$ (LS=1不用算)
  • 证据肯定不出现 P(E)=P(E/S)=0 时：$P(H/\sim E)={LNP(H)\over (LN-1)P(H)+1}$ (LN=1不用算)

Ⅱ非确定性证据：
EH 公式，中间证据计算后验概率 P(H/S)，后用

EH formula

CP 公式，初始证据计算后验概率 P(H/S)，先用

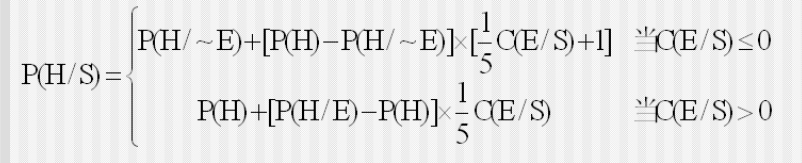
CP formula

若 n 条知识支持同一结论，每条证据 Ei 都有相应的 Si 对应，需要进行合成：首先对每条知识分别求出 $O(H/S_i)$（可 $P(H/S_i)$ 求出），然后使用下面公式求出$O(H/S_i,\cdots,S_n)$，进一步求出 $P(H/S_i,\cdots,S_n)$

o2p

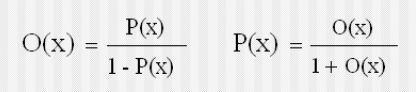
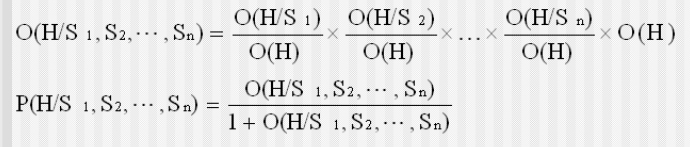
update

已知先验更新出后验证概率的方法参照可信度的公式

D-S证据理论

所有可能的结论的集合为 D，构成 2^n^ 个子集（设任意一子集为 A），2^D^ 表示这些子集的集。命题的结论 y 都会落到某个子集 A 之上，于是用集合 A 表示该命题

概率分配函数 M(x)，满足
$$\sum_{A\subseteq D}M(A)=1,M(\phi)=0$$

信任函数 Bel(x)（下限函数），度量命题 A 为真的信任程度，满足
$$Bel(A)=\sum_{B\subseteq A}M(B)$$

似然函数 Pl(x) （上限函数），度量命题 A 为非假的信任程度，满足
$$Pl(A)=1-Bel(~A)=\sum_{B\cap A\ne\phi}M(B),\quad A\in 2^D$$

概率分配函数正交和，用于合并多个概率分配函数，$M=M_1\oplus M_2$ 的计算如下
$$
\begin{aligned}
&M(\phi)=0\
&M(A)=K^{-1}\times\sum_{x\cap y=A}M_1(x)\times M_2(y)\
&K=\sum_{x\cap y\ne\phi}M_1(x)\times M_2(y)
\end{aligned}
$$
若 K=0，不存在正交，两函数矛盾

基于特定概率分配函数的推理模型
$$f(A)=Bel(A)+{|A|\over|D|}\times[Pl(A)-Bel(A)]$$

知识不确定性以产生式规则的形式表示；H 是结论，是样本空间的子集；ci 对应 hi 的可信度
$$if\quad E\quad then\quad H={h_1,\cdots,h_n}\quad CF={c_1,\cdots,c_n}$$
证据不确定性由 f(E) 表示，当证据是多个证据的合取时，其 f 取当中的最小；析取时取最大
$$
\begin{aligned}
E&=E_1\wedge\cdots\wedge E_n\
f(E)&=min{f(E_1)\cdots f(E_2)}
\end{aligned}
$$

推理计算步骤：
Ⅰ 根据所给知识计算结论 H 的概率分配函数

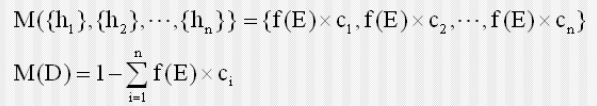
特定概率分配函数

Ⅱ 如果有多条知识支持同一结论，需要正交合成他们的概率分配函数
Ⅲ 求 H 的信任函数 Bel(H) 和似然函数 Pl(H)
Ⅳ 使用推理模型公式计算 f(H)

搜索策略

无信息搜索：盲目搜索，根据事先固定排序调用规则；启发式搜索：跟据可用信息动态确定规则排序

A 算法&A*算法

扩展节点时对 open 表节点按照某个标准进行排序，选取最有“希望”的节点进行扩展

估价函数 $f(n)=g(n)+h(n)$，g(n) 为代价函数，可以通过当前搜索路径算出来（通常指路径长度）；h(n) 为启发函数，某种评价，决定的启发信息的强度。通常估价越低越优先扩展，这就是 A 算法

在 A 算法中，引入$f^(n)=g^(n)+h^(n)$，带星号对应最短路径（隐含）的代价，不带星号的是对带星号的近似。如果满足 $h(n)\le h^(n)$，则该 A 算法变为 A* 算法

A* 算法性质：

  • 可采纳性：如果有解，一定能找到最优解
  • 单调性：若对所有节点 ni 和 nj ，其中 nj 是 ni 的子节点，满足 $h(n_i)-h(n_j)\le c(n_i,n_j),h(s)=0$（构成三角形），则 h(n) 是单调的，此时 A* 算法扩展的节点序列其估价 f 的值是非递减的
  • 信息性：启发信息大的和启发信息小的，前者 h 恒大于后者，后者扩展节点数必不少于前者

与或图搜索

消耗值计算：

  • K-链接符的消耗值为 k
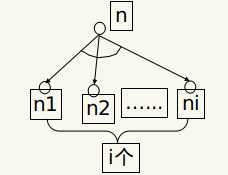
  • 解图消耗值记为 k(n,N)，若 n 是目标节点之一，k(n,N)=0；否则 $k(n,N)=Cn+k(n_1,N)+\cdots+k(n_i,N)$，其中 Cn 为连接符的消耗值
  • 优先选择消耗值小的，在扩展过程中更新消耗值

and-or-graph

博弈算法

极大极小搜索，max 代表我方，min 代表对手；对节点进行估值之后 min 层向 max 层返回最大值，max 层向 min 层返回最小值

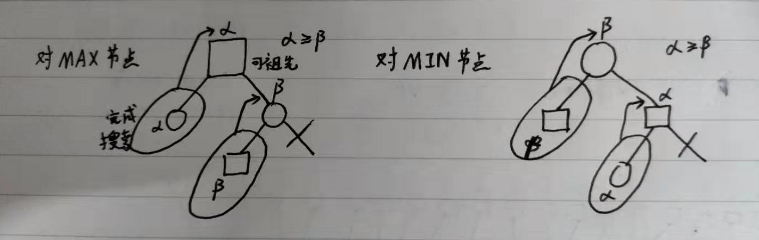
α-β剪枝：

  • 若一个MIN层节点的β值小于或等于它任一先辈MAX层节点的α值，可终止以下该极小值层中这个MIN节点以下的搜索
  • 若一个MAX层节点的α值大于或等于它任一先辈MIN层节点的β值，可终止以下该极大值层中这个MAX节点以下的搜索

α-β

机器学习

学习策略

  • 机器学习：死记，直接根据输入检索出输出
  • 示教学习：执行过程中接受外部建议
  • 类比学习：属性特征提取
  • 示例学习：从正反例中归纳出概念的一般描述

描述空间算法

  • 初始化 H 为整个概念空间，G 集合只包含零描述，S 集合包含所有特例
  • 接受训练例（重复直到 G=S）
    • 如果是正例：从 G 中去除不符合该正例的概念，然后尽可能小地一般化 S 以覆盖该正例
    • 如果是反例：从 S 中去除覆盖该反例的概念，然后尽可能小地特殊化 G 以不覆盖该反例
  • 最后的 G/S 就是所学概念

    添加新评论 | #

    Markdown Supported
    简单数学题：NaN + NaN =
    表情

    Comments | ?? 条评论

    • 单身为狗 25 年

    • 朝循以始 夜继以终

    • Blog: Von by Bersder

    • Alive: 0 天 0 小时 0 分

    Support:

    frame ssr server DNS music player

    © 2019-2024 ᛟᛊᚺᛁᚾᛟ

    back2top